Lab 8: Spectral signature analysis & resource monitoring

Goal

The purpose of this lab is to work with measurement and interpretation techniques for spectral reflectance signatures of various materials in satellite images and to perform basic resource monitoring using remote sensing band ratio techniques. During this exercise, I collected spectral signatures from remotely sensed images, graphed them, and performed analysis on them in order to test spectral separability. This is an important step in image classification. I also monitored the health of vegetation and soils using basic band ratio techniques.

The main goal of this lab was to equip me with the necessary skills to collect and analyze spectral signature curves, specifically in order to monitor the health of vegetation and soils.

Upon completion of this last introductory remote sensing lab, the idea is that I am now equipped with the necessary skills for an entry level remote sensing job, and am also equipped to work on an independent project to complete this class.

Objectives

1.       Spectral signature analysis

2.       Resource monitoring

·         Vegetation health monitoring

·         Soil health monitoring

·         Prepare a map to show mineral distribution

Part 1: Spectral signature analysis

In this part of the lab, you are going to use a Landsat ETM+ image (taken in 2000) that covers the Eau Claire area and other regions in WI, and MN to collect and analyze spectral signatures of the following earth features:

1. Standing Water

2. Moving water

3. Vegetation

4. Riparian vegetation.

5. Crops

6. Urban Grass

7. Dry soil (uncultivated)

8. Moist soil (uncultivated)

9. Rock

10. Asphalt highway

11. Airport runway

12. Concrete surface (Parking lot)

The Field Spectrometer Pro instrument takes reflectance measurements in the visible, Near-Infrared and Mid-Infrared regions of electromagnetic spectrum (0.4 – 2.5 μm).

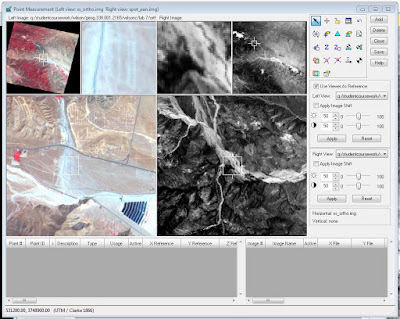
The first spectral signature collected was from Lake Wissota, located in the north-northeast part of Eau Claire. Using the polygon tool (under Home>Drawing), I selected an AOI inside Lake Wissota (Fig. 1). I then opened the Signature Editor (Raster>Supervised>Signature Editor) and graphed the spectral curve of this standing water signature (Fig. 2). The water curve is characterized by high absorption at near infrared wavelengths range and beyond, which is why the signature curve shows such low reflectance at 0.4 and above.

Figure 1. The selected area of Lake Wissota near Eau Claire, Wisconsin provided the spectral signature for the Standing Water category.

Figure 2. From the signature mean plot of standing water, I gathered that the band with the highest reflectance was 0.1 and the band with the lowest reflectance was 0.4 micrometers, though 0.6 was also comparably low.

I continued to select areas from the photo to represent the other 11 categories, using Google Earth imagery as ancillary data. The Signature Editor window (Fig.3) displays the other categories and their details. These were compiled into the Spectral Signature graph (Fig.4).

Figure 3. The Signature Editor window containing the twelve categories. 

Figure 4. Comparing the spectral signatures of the different materials gives us a rounded understanding of which bands (layers) provide the largest distinction between reflection levels of the different materials. 

Part 2: Resource monitoring

Section 1: Vegetation health monitoring

In this section of the lab, I performed a band ratio on the ec_cpw_2000.img image by implementing the normalized difference vegetation index (NDVI).

Using the Raster>Unsupervised>NDVI tool to open the Indices interface, I used the ‘Landsat 7 Multispectral’ sensor to generate an NDVI image. Unfortunately, the ERDAS software had a malfunction before I could take a screenshot of my NDVI image. 

Section 2: Soil health monitoring

For this final section, I used simple band ratio by invoking the ferrous mineral

ratio on the ec_cpw_2000.img image (Fig.5) to monitor the spatial distribution of iron contents in soils within Eau Claire and Chippewa counties (Fig. 6).

Figure 5. Eau Claire and Chippewa Counties in false color. This was the image used in both parts of Lab 8.

Figure 6. The final product was this image depicting Ferrous Mineral deposits in white. Notice that the distribution of these minerals are on the west side of the Chippewa River.

Sources

Data for this lab exercise was provided to the students of Geography 338: Remote Sensing of the Environment by Dr. Cyril Wilson, Professor of Geography at University of Wisconsin Eau Claire.

Satellite image is from Earth Resources Observation and Science Center, United States Geological Survey.

Lab 7: Photogrammetry

Goals and Background

The main goal of this laboratory exercise is to practice key photogrammetric tasks on aerial photographs and satellite images. Specifically the lab is designed to better understanding of the math behind the calculation of photographic scales, the measurement of areas and perimeters of features, and calculating relief displacement. Furthermore, we were introduced to the important processes of stereoscopy and orthorectification on satellite images. The output of this lab was to be a 3D image using an elevation model. 

Methods

Scales, measurements and relief displacement

For an exercise on Stereoscopy, I calculated the scale of an aerial image using the photo distance. I also compared two images and found examples of relief displacement in one of them and took measurements of areas of features on aerial photographs.

Stereoscopy

In this part of the lab, I used one form of ground control points (GCP) to show a 3D perspective of the City of Eau Claire.  I viewed two images: a digital elevation model (DEM) of the City of Eau Claire at 10 meter spatial resolution and an image of the City of Eau Claire at 1 meter spatial resolution. Using Anaglyph Generation under the Terrain tab in ERDAS, I generated an anaglyph from the two images and then viewed it in ERDAS wearing polaroid glasses provided in the campus geography lab.

Next I opened an image of the City of Eau Claire and adjacent jurisdictions at 1 meter spatial resolution called “eau_claire_quad.img” and also a LiDAR-derived digital surface model (DSM) of the City of Eau Claire at 2 meter spatial resolution. I made an anaglyph image from them using the Anaglyph Generation like in the previous step.  Comparing the two revealed that the latter method, using an anaglyph image made with LiDAR DSM instead of a DEM, provides much better 3D results. 

Orthorectification

This section of the lab was designed to introduce us to Erdas Imagine Lecia Photogrammetric Suite (LPS), which is used in digital photogrammetry to complete many functions, such as triangulation, orthorectification, extraction of digital surface and elevation models, and much more. We uses LPS to orthorectify images and in the process create a planimetrically true orthoimage.  

We used data that covered part of Palm Springs, California.

We used already orthorectified images as a source for ground control measurements. The first, XS_ortho.img is a SPOT image, and the second, NAPP_2m-ortho.img is an aerial photo. Using these images I built a block consisting of two images with 10-meter resolution.

Tasks For Orthorectification: 

• Create a new project.
• Select a horizontal reference source.
• Collect GCPs.
• Add a second image to the block file.
• Collect GCPs in the second image.
• Perform automatic tie point collection.
• Triangulate the images.
• Orthorectify the images.
• View the orthoimages.
• Save the block file.

Earlier in the process I created a new project using SPOT satellite images of Palm

Springs, California.

Figure 1 The Point Measurement tool automatically changes to display the reference image xs_ortho, in the left view of the point measurement tool, and the original image, spot_pan, in the right view.

I then collected reference coordinates by selecting points in the reference image that correspond to points in the block image, spot_pan. I collected GCPs and identify their X and Y coordinates. 

The reference coordinates were selected in xs_ortho, the reference image that corresponds to points in the block image, spot_pan.

 I added two points manually, then used the the Automatic (x,y) Drive tool to allow LPS Project Manager to approximate the position of a GCP in the block image file, spot_pan based on the position in the reference image, xs_ortho, which made the process much more efficient.

I set the elevation information using data from the digital elevation model (DEM) file labeled palm_springs_dem.img using the Vertical Reference Source. I then set the Type and Usage for each of the control points, added a second image to the block file and collected tie points. 

Figure 2 Using the formula option in the Column Options menu, I changed the Type on all twelve points to “Full” and the Usage to “Control.”

I then added SPOT_panb as a frame and added GCPs based on those I had already collected in

spot_pan.

Figure All of the GCPs from SPOT_pan have been added to SPOT_panb.

Automatic tie point collection, triangulation and ortho resample

Now I completed the orthorectification process of the two images in the block, spot_pan and spot_panb through several processes. I collected tie points to measure the image coordinate positions of GCPs appearing on the overlapping area of the two SPOT images. I checked a sample of three of the tie points and found them sufficiently accurate.

Figure This is the photogrammetry manager now shows with the GCPs being present on both pan images.

With all the control and tie points, I initiated triangulation to establish the mathematical relationship between the images that make the block file, the sensor model, and the ground.

Figure This report summarizes the results of the triangulation function. 

Figure Notice that the Ext. columns in the cell array in the IMAGINE Photogrammetry Project Manager are now green. This indicates that the exterior orientation information has been supplied.

Results

In my newly orthorectified images, relief displacement and other geometric errors were sufficiently removed and accuracy was significantly improved. The orthorectified images display the photographed objects in their real-world X and Y positions and their coordinates are reliable for navigation and mapping.

Figure The final image shows the finished product; the orthorectified image is seamless.

Data Sources

Orthorectification lab was modified from Erdas Imagine LPS user guide developed for version 8.7 (2005).

The data used in this lab was provided by Dr. Cyril Wilson and collected from the following sources: NAIP in 2005 (image of Eau Claire county), aerial images of Palm Springs, California.

Lab 6: Geometric Correction

Goal

The goal of this lab was to introduce us to the preprocessing skill of geometric correction. The lab was structured to develop our skills on the two major types of geometric correction: Image-to-map and image-to-image rectification through polynomial transformation.

Objectives:

1.      Use a 7.5 minute digital raster graphic (DRG) image of the Chicago Metropolitan Statistical Area to correct a Landsat TM image of the same area using ground control points (GCPs) from DRG to rectify the TM image.

2.      Use a corrected Landsat TM image for eastern Sierra Leone to rectify a geometrically distorted image of the same area.

Methods

Image-to-Map Rectification

I opened the provided Chicago.drg.img, which is a USGS 7.5 minute digital raster graphic covering part of Chicago (see figure 1).

Figure 1 This is a USGS 7.5 minute digital raster graphic (DRG) covering part of the Chicago region and adjacent areas. The subset is to show detail.

To rectify the image Chicago_2000 to the Chicago DRG, I used the Multipoint Geometric

Correction tool under Multispectral/Ground Control Points in the ERDAS Imagine interface. The Multipoint Geometric Correction window contains 2 panes. On the left is the input image (Chicago_2000.img), while the reference image is on the right pane (Chicago_drg.img). Each of these panes contains three windows. The top left and top right panes show the entire input and reference images respectively. The other two central top panes shows the areas that are zoomed into on the input image and also that zoomed into on the reference image.

See figure two for a close up view.

Figure 2 The Multipoint Geometric Correction window with the input image (Chicago_2000.img) and reference image (Chicago_drg.img). 

I chose four sets of ground control points (GCPs) to align the aerial image “Chicago_2000.img” with the reference image (“chicage_drg.img”). Though only three GCPs are necessary for a first order polynomial, it is wise to collect more than the minimum required GCPs in geometric correction in order for the output image to have a guaranteed good fit. Figure 3 displays the Multipoint Geometric Correction window. The table at the bottom indicates the RMS (Root Mean Square) Error for the individual points and for the image in total. Notice the RMS error is below 0.5, which means the ground control points are accepted as accurate by industry standards.

Figure 3 The Multipoint Geometric Correction window after placement of the ground control points. The RMS Error is less than 0.5. 

For further explanation of the process, Chicago_drg.img served as the reference map to which we rectified/georeferenced the Chicago_2000 image. Using points from the reference image, a list of GCPs were created that were used to register the aerial image to the reference image in a first order transformation. This works to anchor the aerial image down to a known location; the reference image already had a known source and geometric model. We then used a computed transformation matrix to resample the unrectified data.

The interpolation used was the nearest neighbor method wherein each new pixel in the output image is assigned to the pixel nearest it in the input image.

Matrices consist of coefficients that are used in polynomial equations to convert the coordinates of the input image. A 1st-order transformation was used because the aerial image was already projected onto a plane but not rectified to the desired map projection.

Image-to-Image Rectification

Part two involved doing the rectification process again, this time with two images instead of an image and a map. A third order polynomial transformation was required because of the extent of the distortion, and third order transformations require at least 10 GCPs.

For further explanation of higher order transformations, click here. 

Figure 4 The Image-to-image transformation with twelve GCPS. Notice that the total RMS Error is below 0.05.

Results

Through this laboratory exercise, I developed skills in Image-To-Map and Image-to-Image rectification methods of geometric correction. This type of preprocessing is one that is commonly performed on satellite images before data or information is extracted from the satellite image. The results of the rectification processes can be seen below in figures five and six.

   Figure 5 The image-to-map rectified image of Chicago and the surrounding area.

Figure 6 My rectified image compared to the Sierra Leone image that was used as the reference in the transformation process. The color of my image is washed out, but the orientation appears accurate.

Data sources

Data used in this lab was provided by Dr. Cyril Wilson and collected from the following sources:

 Satellite images are from Earth Resources Observation and Science Center, United States

Geological Survey.

Digital raster graphic (DRG) is from Illinois Geospatial Data Clearing House.

LiDAR Remote Sensing

Goal and Background

 LiDAR is a rapidly growing geospatial technology and the increasing market for it has many implications for the future of imagery and image collection. The goal of this lab exercise was to practice basic skills involved in processing LiDAR data, particularly using LiDAR point clouds in LAS file format. Objectives of this lab included processing and retrieval of various surface and terrain models, and processing of intensity images and point cloud-derived products. We were told to imagine this exercise in the context of a GIS manager working on a project for the city of Eau Claire.

Objectives

1. Acquire LiDAR point cloud in LAS format for a portion of the City of Eau Claire.
2. Initiate an initial quality check on the data by looking at its area and coverage, and also verify the current classification of the LiDAR.
3. Create a LAS dataset
4.  Explore the properties of LAS dataset
5. Visualize the LAS dataset as point cloud in 2D and 3D
6. Generate LiDAR derivative products

Methods

In part one, I download point cloud data into Erdas Imagine and accessed the tile index file specified for the lab. It is a point cloud dataset of Eau Claire. I selected the same section in ERDAS and ArcMap for practice.

I performed a QA/QC check by comparing the minimum and maximum Z points to the known elevation. The dataset was displayed in tiles.

Part two focused on generating a LAS dataset and exploring LiDAR point clouds with ArcGIS. I created a new LAS dataset in ArcCatalogue. LAS data comprises a great deal of information in the header files associated with the data and there is also ancillary data that can be accessed as well. Using the external metadata, I assigned the D_North_American_1983 and North American Vertical Datum of 1988 to the dataset. For reference, I added a shapefile of Eau Claire County (see Figure 1), which was deleted afterwards.

Figure 1 The grid highlights the area covered by the pointcloud dataset of the city of Eau Claire as compared to the greater Eau Claire County.

The default display settings are point color codes according to elevation, using all returns. Figure 2 shows the elevation range and a portion of the dataset.

Figure 2 A section of the dataset displaying elevation of all returns.

Below are four different views of the data; Elevation, Aspect, Slope, and Contour (see Figure 3).

Figure 3 Four different views of the same subset of the LAS dataset, each displaying a different element.

Next I explored the point clouds according to Class, Return and profile. In ArcMap there is the option to display selected features in 2D and 3D models for more thorough visualization.

Part three involved the generation of Lidar derivative products. In order to derive DSM and DTM products from point clouds, I estimated the average nominal pulse spacing (NPS) at which the point clouds were collected. The derived image below (Figure 4) is the result of  inputting the LAS dataset into the LAS dataset to Raster tool and using the binning interpolation method with a maximum cell type and a natural neighbor void filling method.

Figure 4 The derived raster converted from the LAS dataset using the LAS dataet to Raster tool in ArcMap.

Using the LAS Dataset to Raster and Hillshade tools, I then created the following derivative products:

• Digital surface model (DSM) with first return
• Digital terrain model (DTM)
• Hillshade of the DSM (see Figure 5)
• Hillshade of the DTM (see Figure 6)

Figure 5 The hillshade results of the first return elevation model performed on the derived raster.

Figure 6 The hillshade results of the terrain model (ground returns only) of the derived raster.

Finally, a lidar intensity image was generated following a similar procedure used to create the DSM and DTMs above. The image was displayed in ERDAS to enhance its appearance automatically.

Results

Through this exercise I learned how to use Lidar data and gained familiarity with some processing toold in ArcMAP. I processed surface and terrain models and used Lidar derivative products as ancillary data in order to improve image classification of the remotely sensed imagery. The final output image was an intensity image of the point cloud data (see Figure 7).

Figure 7 A high intensity image produced with the LAS dataset from the city of Eau Claire.

Data sources

The Lidar point cloud and Tile Index data are from the Eau Claire County 2013 and the Eau Claire County shapefile is from Mastering ArcGIS 6th Edition data by Margaret Price 2014. All data was provided by Dr. Cyril Wilson of the University of Wisconsin- Eau Claire.

Remote Sensing Lab 4

Introduction to Lab 4: Miscellaneous Image Functions

This seven part lab was designed to acquaint us students to various functions and processes that can be performed on aerial images. There were multiple objectives for this lab, including: selecting and clipping an area of interest from a larger satellite image, learning about optimization of spatial resolution, and practice with linking a satellite image to Google Earth as ancillary information. This lab also served as an introduction to binary change detection, image mosaicking, common resampling methods, and various radiometric enhancement techniques such as haze reduction.

Methods

Aerial images and data was provided for us.  

Part one of the lab was to create a subset of the Eau Claire area from a larger satellite image using first the Inquire Box method, and then by delineating using a shapefile (see Results Figure 1 under Results).

In part two, the spatial resolution of an image was increased using image fusion pansharpening. An aerial photo of Eau Claire and Chippewa counties from the year 2000 with a resolution of 30 meters was pansharpened using a resolution merge with a 15 meter panchromatic image. I used a multiplicative method and a nearest neighbor resampling technique.

In part three, I removed haze from an aerial photo of Eau Claire using the Haze Reduction tool under radiometric enhancement techniques in ERDAS Imagine.

In part four I opened Google Earth through ERDAS Imagine and linked it to an aerial image of Eau Claire to use as ancillary information.

For part five, an aerial photo of Eau Claire with a resolution of 30 meters was resampled to 15 meter resolution by using the nearest neighbor method, and then again using bilinear interpolation. Both of these methods were under “Resample Pixel Size” under the Spatial raster tool.

Part six focused on image mosaicking. Two compatible rasters were brought into ERDAS Imagine (see Figure A below) and mosaicked first through the use of the Mosaic Express function and then through the use of Mosaic Pro. See Results Figure 3 to view the comparison.

Fig. A Two rasters in the process of being mosaicked with the Mosaic Express tool.

For part seven I created a difference image to highlight change that has occurred in Eau Claire and four neighboring counties by comparing a 1991 image to a 2011 image using Two Image Functions and input operators interface under the Functions raster tool. I ascertained the cutoff threshold points by adding the mean to the standard deviation value x 1.5. I drew these values onto the histogram, as you can see in figure B below.

Fig. B The histogram from part seven labelled with the cutoff threshold values.

Using the equation ΔBVijk = BVijk(1) – BVijk(2) + c and Model Maker, I created a model to subtract the 1991 image from the 2011 image (figure C below).

Fig. C 

I then created a second model to command Imagine to show all pixels with values above the no change threshold value and mask out those that are below the no change threshold value (figure D).

Fig. D

I opened the output images that the models generated in ArcMap and made a map of the changes that were detected (see Results Figure 3).

Results

Results Fig. 1 The area of interest as a subset of the original image from part one.

Results Fig. 2 Comparison of mosaics done by Mosaic Express and Mosiac Pro.

Results Fig. 3

Sources

Satellite images are from Earth Resources Observation and Science

Center, United States Geological Survey. 

 Earth Resources Observation and Science (EROS) Center. U.S. Department of the Interior, U.S. Geological Survey. (2016, April 16). Retrieved May 20, 2016, from http://eros.usgs.gov/ 

Shapefile is from Mastering ArcGIS 6th edition Dataset

by Maribeth Price, McGraw Hill. 2014.